GEOMETRÍA SAGRADA

El concepto de la geometría sagrada es un tema amplio con fronteras difusas del que todo aquel que tiene algo para decir, lo hace aportando su contexto y pretexto, de acuerdo a sus creencias y ámbito de estudio. En este caso, que no puedo decir que será la excepción, intentaré ser lo más pragmático posible, recortando lo que yo entiendo es relevante transmitir por sobre lo que no es.

La geometría sagrada es la creencia de que existe una lógica matemática, geometría y física que subyace todo lo existente en el universo. Es la idea de que existe un patrón de creación preciso e ininmutable, una manera deliberada y exacta en que se organiza la energía, en todas sus formas. En este sentido, la Geometría Sagrada sería una meta-estructura con la que está construida, literalmente, la materia.

Este patrón constituiría la evidencia de una "Conciencia Creadora", ya que lejos de resultar al azar, la creación utiliza determinados parámetros, fórmulas y ratios. Desde un minúsculo átomo hasta la más inmensa galaxia, todo responde a un mismo diseño matemático/geométrico.

La cantidad y disposición de los pétalos en una flor, la morfología de un cristal de hielo, las escamas de las piñas de pino, la concha de un nautilus, las órbitas de planetas, las espirales de las galaxias, y muchos etc. más, son manifestaciones de este código geométrico maestro.

A lo largo de la historia se han ido descifrando algunos conceptos de lo que, para algunos, son los fragmentos de este diseño maestro, las piezas "Rasti" de la creación. En otros casos se trata de meras especulaciones supersticiosas, sin mayor criterio analítico.

A continuación: Phi, Pi, Los Sólidos Platónicos, La Flor de la Vida, y Toroides

Phi: El número áureo y Fibonacci

El número áureo (también llamado número de oro, razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) es un número irracional representado por la letra griega Phi (Φ, φ) y su fórmula es:

{\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}\approx 1,6180339887498948...}

El número fue descubierto en la antigüedad, no como una expresión aritmética, sino como relación o proporción entre dos segmentos de una recta, es decir, una construcción geométrica.

La proporción áurea es aquella que guardan entre sí dos segmentos de recta a y b (a más largo que b), que cumplen la siguiente relación: La longitud total "a+b" es al segmento más largo "a", como "a" es al segmento más corto "b"; que matemáticamente se traduce en (a+b)/a = a/b.

El número áureo surge de la división en dos de un segmento guardando las siguientes proporciones: La longitud total **a+b**es al segmento más largo a, como a es al segmento más corto b. Imagen: Wikipedia

El ángulo áureo es el que se obtiene al dividir una circunferencia en proporción áurea y resulta ser de unos 137,5º.

Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea, a punto tal que algunos incluso creen que posee una valor místico. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura, esculturas y artes plásticas.

Video y animación de Cristobal Vial

Historia del número áureo

Algunos autores sugieren que el número áureo se encuentra como proporción en varias estelas de Babilonia y Asiria de alrededor de 2000 AEC. Sin embargo, no existe documentación histórica que indique que el número áureo fuera utilizado conscientemente por dichos artistas en la elaboración de las estelas.

El primero en hacer un estudio formal del número áureo fue Euclides (c. 300-265 AEC), quien lo definió de la siguiente manera:

Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor [Los Elementos Definición 3 del Libro Sexto].

Euclides demostró también que este número no puede ser descrito como la razón de dos números enteros; es decir, es un número irracional. Platón consideró que los números irracionales, descubiertos por los pitagóricos, eran de particular importancia y la llave de la física del cosmos. Esta opinión tuvo una gran influencia en muchos filósofos y matemáticos posteriores, en particular los neoplatónicos.

El astrónomo Johannes Kepler (1571-1630) desarrolló un modelo platónico del sistema solar utilizando los sólidos platónicos, y se refirió al número áureo en términos grandiosos en su Mysterium Cosmographicum (El misterio cósmico):

La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de plata; el segundo lo debemos denominar una joya preciosa.

El primer uso conocido del adjetivo áureo, dorado, o de oro, para referirse a este número lo hace el matemático alemán Martin Ohm, hermano del célebre físico Georg Simon Ohm, en la segunda edición de 1835 de su libro Die Reine Elementar Matematik (Las matemáticas puras elementales):

Uno también acostumbra llamar a esta división de una línea arbitraria en dos partes como éstas la sección dorada.

En los textos de matemáticas que trataban el tema, el símbolo habitual para representar el número áureo fue τ, del griego τομή, que significa 'corte o sección'. Sin embargo, la moderna denominación Φ o φ la efectuó en 1900 el matemático Mark Barr en honor a Fidias (Φειδίας) por el máximo valor estético atribuido a sus esculturas, propiedad que ya por entonces se le atribuía también al número áureo.

Propiedades aritméticas y geométricas de Phi

Φ {1,618033988749894848204586834365638117720309…} es el único número real positivo tal que:

φ posee además las siguientes propiedades, derivadas de la anterior:

\varphi ^{3}={\frac {\varphi +1}{{\varphi -1}}}\

{\displaystyle \varphi ^{2}-{\frac {1}{\varphi }}=2\ }

Las potencias del número áureo pueden expresarse en función de una suma de potencias de grados inferiores del mismo número, establecida una verdadera sucesión recurrente de potencias. El caso más simple es:

{\displaystyle \varphi ^{n}=\varphi ^{n-1}+\varphi ^{n-2}\,}

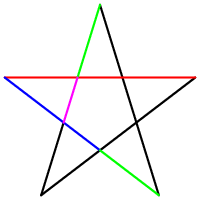
El número áureo tiene un papel muy importante en los pentágonos regulares y en los pentagramas. Cada intersección de partes de un segmento se interseca con otro segmento en una razón áurea. El pentagrama incluye 10 triángulos isóceles (5 acutángulos y 5 obtusángulos). En todos, la razón de lado mayor y el menor es φ, y se conocen como triángulos áureos. Dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad infinita.

Los segmentos coloreados del pentagrama poseen proporciones áureas. Imagen: Wikipedia

Sucesión de Fibonacci

La sucesión de Fibonacci o secuencia áurea es la sucesión infinita de números naturales 0,1,1,2,3,5,8,13,21,34… de modo que la relación de recurrencia que la define es que cada término es la suma de los dos anteriores.

Al construir bloques cuya longitud de lado sean números de Fibonacci se obtiene un dibujo que se asemeja al rectángulo áureo. Imagen: Wikipedia

La particularidad de esta secuencia es que, al dividir un número por su anterior inmediato, nos da como resultado un número que, cuanto más avanzado esté en la serie, más aproximado es a Phi (1,618).

Si se denota el enésimo número de Fibonacci como F_n, y al siguiente número de Fibonacci como F_{n + 1}, descubrimos que, a medida que n aumenta, esta razón oscila y es alternativamente menor y mayor que la razón áurea. Entonces se tiene que:

{\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi }

Esta sucesión fue descrita por el matemático italiano Leonardo de Pisa, también conocido como Fibonacci, en su libro Liber Abaci, publicado en 1202. Pero mucho antes de ser conocida en occidente esta sucesión ya estaba descrita en la matemática en la India, atribuyéndose parte del desarrollo de la misma a Pingala (año 200).

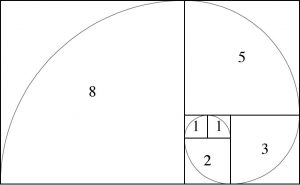
La espiral de Fibonacci: una aproximación de la espiral áurea generada dibujando arcos circulares conectando las esquinas opuestas de los cuadrados ajustados a los valores de la sucesión; adosando sucesivamente cuadrados de lado 0, 1, 1, 2, 3, 5, 8, 13, 21 y 34. Imagen: Wikipedia

El número áureo en la naturaleza

Esta proporción áurea se puede hallar "aplicada" en la naturaleza en diversos casos:

La disposición de los pétalos de las flores (el papel del número áureo en la botánica recibe el nombre de Ley de Ludwig).

En la cantidad de elementos constituyentes de las espirales o dobles espirales de las inflorescencias, como en el caso del girasol, se encuentran números pertenecientes a la sucesión de Fibonacci.

La cantidad de espirales de una piña (ocho para un lado, y trece para el otro).

La disposición de las hojas del col

La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol o de cefalópodos, como el nautilus.

La explicación lógica es que, para que las hojas esparcidas de una planta o las ramas alrededor del tronco tengan el máximo de insolación con la mínima interferencia entre ellas, éstas deben crecer separadas en hélice ascendente según un ángulo constante lo más cercano a 137º 30′ 27,95″ [360º x (2 – φ)].

Este hecho fue descubierto empíricamente por Church y confirmado matemáticamente por Weisner en 1875. En la naturaleza, las plantas reproducen este ángulo óptimo "orgánicamente".

Otros casos de la elipse áurea en la naturaleza, a una escala mayor:

Vista aérea de la formación de un huracán

Vista de una galaxia con forma de doble espiral

Sucesión de Fibonacci en la naturaleza

También se puede encontrar la serie de Fibonacci aplicada en las nervaduras de las hojas de algunos árboles y en el grosor de sus ramas:

La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a Φ tomando como unidad la rama superior).

La relación entre las nervaduras de las hojas de los árboles.

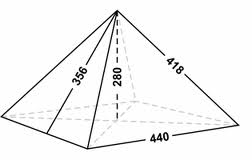
El número áureo en la pirámide de Giza

La Gran Pirámide de Giza guarda varias relaciones áureas en sus medidas. De acuerdo con las medidas originales de la pirámide de Kheops, es decir 440 codos reales (230,40 metros) de longitud media de base (perímetro) y 280 codos reales (146,60 metros) de altura original, se da que:

Dos lados dividido la altura da como resultado el número Pi
(π) con un margen de error de ±0.04%: 2 x 440 / 280 = 3,14

El apotema dividido medio lado da como resultado Phi (Φ)
con un margen de error de ±0.03%: 356 / (440 / 2) = 1,618.

La superficie de sus 4 lados dividido la superficie de la base también es igual a Phi (Φ): ((440 x 356 / 2) x 4) / (440 x 440) = 1,618.

Sería razonable que una construcción de semejante tamaño contenga errores propios a toda obra arquitectónica, más aún al estado de la tecnología de ese momento. No obstante, la exactitud lograda es mucho más que lo esperable. Esta utilización arquitectónica del número de oro es la más antigua que se conoce hasta el momento.

Algunos estudios, como los del Dr. Fechner, han argumentado que la percepción de la belleza radica en la proporción áurea. Esta noción de belleza y proporción ha sido aplicada a estructuras arquitectónicas, pinturas, partituras musicales, entre otras cosas.

Pi

π (pi) es la relación entre la longitud de una circunferencia y su diámetro en geometría euclidiana. Es un número irracional (no puede expresarse como fracción de dos números enteros) y una de las constantes matemáticas más importantes, junto con el número e. El valor numérico de sus primeras cifras es: 3.14159265358979323846

La notación con la letra griega π proviene de la inicial de las palabras de origen griego περιφέρεια 'periferia' y περίμετρον 'perímetro' de un círculo, notación que fue utilizada primero por William Oughtred (1574-1660) y cuyo uso fue propuesto por el matemático galés William Jones (1675-1749); aunque fue el matemático Leonhard Euler, con su obra Introducción al cálculo infinitesimal, de 1748, quien la popularizó.

Ciertamente, una constante muy estudiada desde los inicios de la civilización:

Año	Matemático o documento	Cultura	Aproximación	Error (en partes por millón)
~1900 a. C.	Papiro de Ahmes	Egipcia	2⁸/3⁴ ~ 3.1605	6016 ppm
~1600 a. C.	Tablilla de Susa	Babilónica	25/8 = 3.125	5282 ppm
~600 a. C.	La Biblia (Reyes I, 7:23)	Judía	3	45 070 ppm
~500 a. C.	Bandhayana	India	3.09	16 422 ppm
~250 a. C.	Arquímedes de Siracusa	Griega	entre 3 10/71 y 3 1/7 empleó 211875/67441 ~ 3.14163	<402 ppm 13.45 ppm
~150	Claudio Ptolomeo	Greco-egipcia	377/120 = 3.141666…	23.56 ppm
263	Liu Hui	China	3.14159	0.84 ppm
263	Wang Fan	China	157/50 = 3.14	507 ppm
~300	Chang Hong	China	10^1/2 ~ 3.1623	6584 ppm
~500	Zu Chongzhi	China	entre 3.1415926 y 3.1415929 empleó 355/113 ~ 3.1415929	<0.078 ppm 0.085 ppm
~500	Aryabhata	India	3.1416	2.34 ppm
~600	Brahmagupta	India	10^1/2 ~ 3.1623	6584 ppm
~800	Al-Juarismi	Persa	3.1416	2.34 ppm
1220	Fibonacci	Italiana	3.141818	72.73 ppm
1400	Madhava	India	3.14159265359	0.085 ppm
1424	Al-Kashi	Persa	2π = 6.2831853071795865	0.1 ppm

Euclides fue el primero en demostrar que la relación entre una circunferencia y su diámetro es una cantidad constante. No obstante, existen diversas definiciones del número Pi, pero las más común es: Pi es la razón entre la longitud de cualquier circunferencia y la de su diámetro.

De lo que surgen sus dos fórmulas más básicas:

Longitud de la circunferencia de radio r: C = 2 π r
Área del círculo de radio r: A = π r²

En la era actual, gracias a la evolución de la tecnología, se conocen más de 10 billones de decimales de Pi. Todos los ensayos estadísticos realizados sobre la sucesión de los dígitos decimales de pi han corroborado su carácter aleatorio, no hay orden ni regularidad.

Por esto, sus series de repeticiones del mismo número intrigan a los estudiosos:

8 repeticiones: 3, 5, 0
9 repeticiones: 1,2,4,7,8,9
10 repeticiones: solo el 6, que aparece en el decimal 386,980,412

Algo que también llama la atención de Pi es que, además de estar relacionado con geometría circular, hay otras fórmulas que lo contienen sin mayor relación aparente.

En probabilidad y estadística:

La probabilidad de que dos enteros positivos escogidos al azar sean primos entre sí es: 6/π²
Si se eligen al azar dos números positivos menores que 1, la probabilidad de que junto con el número 1 puedan ser los lados de un triángulo obtusángulo es: (π-2)/4
El número medio de formas de escribir un entero positivo como suma de dos cuadrados perfectos es π/4 (el orden es relevante).

En física:

Principio de incertidumbre de Heisenberg: En mecánica cuántica, la relación de indeterminación de Heisenberg o principio de incertidumbre establece la imposibilidad de que determinados pares de magnitudes físicas observables y complementarias sean conocidas con precisión arbitraria. Sucintamente, afirma que no se puede determinar, en términos de la física cuántica, simultáneamente y con precisión arbitraria, ciertos pares de variables físicas, como son, la posición y el momento lineal (cantidad de movimiento) de un objeto dado. En otras palabras, cuanta mayor certeza se busca en determinar la posición de una partícula, menos se conoce su momento lineal y, por tanto, su masa y velocidad. Este principio fue enunciado por Werner Heisenberg en 1927.

\Delta x\,\Delta p\geq {\frac {h}{4\pi }}

Ley de Coulomb para la fuerza eléctrica: La ley de Coulomb, que enunció en 1785, forma la base de la electroestática y puede expresarse como: La magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales en reposo es directamente proporcional al producto de la magnitud de ambas cargas e inversamente proporcional al cuadrado de la distancia que las separa y tiene la dirección de la línea que las une. La fuerza es de repulsión si las cargas son de igual signo, y de atracción si son de signo contrario.

F={\frac {\left|q_{1}q_{2}\right|}{4\pi \varepsilon _{0}r^{2}}}

Permeabilidad magnética del vacío: En física se le denomina permeabilidad magnética a la capacidad de una sustancia o medio para atraer y hacer pasar a través de ella campos magnéticos, la cual está dada por la relación entre la inducción magnética existente y la intensidad de campo magnético que aparece en el interior de dicho material. La permeabilidad del vacío, conocida también como constante magnética, se representa mediante el símbolo μ₀ y se define como:

\mu _{0}=4\pi \cdot 10^{{-7}}\,{\mathrm {N/A^{2}}}\,

A modo de curiosidad, el versículo 3.14 del Libro del Éxodo de la Torá es bastante particular ya que en él Dios revela su nombre a Moisés:

Éxo. 3.14. Y respondió Dios a Moisés: YO SOY EL QUE SOY. Y dijo: Así dirás a los hijos de Israel: YO SOY me envió a vosotros.
[De aquí el origen del nombre divino YHWH, que se relaciona con el verbo hayah, "ser".]

Los Sólidos Platónicos

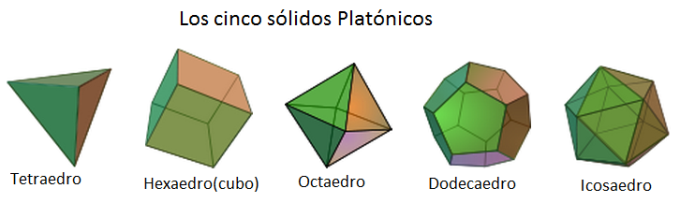
Platón (427 AEC – 347 AEC) se ocupó de estudiar el origen y la estructura del cosmos e imaginó que estaba conformado por cinco formas o sólidos: el tetraedro, el cubo (o hexaedro regular), el octaedro (o bipirámide cuadrada), el dodecaedro y el icosaedro (o bipirámide pentagonal).

Los Sólidos Platónicos son poliedros regulares, convexos donde las caras son polígonos regulares congruentes, con el mismo número de caras en cada vértice.

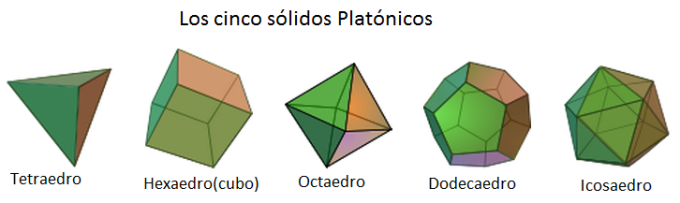
Esta lista es exhaustiva, ya que es imposible construir otro sólido diferente de los cinco anteriores que cumpla todas las propiedades exigidas, es decir, convexidad y regularidad.

Los sólidos platónicos tienen caracterizaciones simétricas: sus centros de simetría equidistan de sus caras, vértices y aristas; poseen simetría axial y simetría especular respecto de una serie de planos que los dividen en dos partes iguales.

Se le atribuye la formulación de la teoría general de los poliedros regulares a Teeteto, matemático contemporáneo de Platón. Este último combinó la idea de Empédocles sobre la existencia de cuatro elementos básicos de la materia, con la teoría atómica de Demócrito.

Para Platón, cada uno de estos sólidos correspondía a una de las partículas que conformaban cada uno de los elementos básicos del universo. Timeo de Locri, en el diálogo de Platón, dice:

«El fuego está formado por tetraedros; el aire, de octaedros; el agua, de icosaedros; la tierra de cubos; y como aún es posible una quinta forma, Dios ha utilizado ésta, el dodecaedro pentagonal, para que sirva de límite al mundo».

Relación con el número áureo

El número áureo está relacionado con los sólidos platónicos, en particular con el icosaedro y el dodecaedro, cuyas dimensiones están dadas en términos del número áureo.

Los 12 vértices de un icosaedro con aristas de longitud 2 pueden expresarse en coordenadas cartesianas por los siguientes puntos:

(0, ±1, ±φ), (±1, ±φ, 0), (±φ, 0, ±1)

Los 20 vértices de un dodecaedro con aristas de longitud 2/φ=√5−1 también se pueden dar en términos similares:

(±1, ±1, ±1), (0, ±1/φ, ±φ), (±1/φ, ±φ, 0), (±φ, 0, ±1/φ)

Si tres rectángulos áureos se solapan paralelamente en sus centros, los 12 vértices de los tres rectángulos áureos coinciden exactamente con los vértices de un icosaedro, y con los centros de las caras de un dodecaedro. El punto que los rectángulos tienen en común es el centro tanto del dodecaedro como del icosaedro.

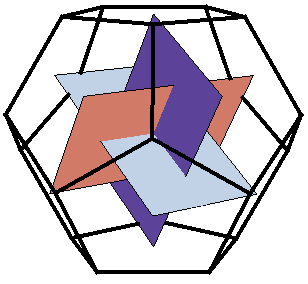
Los 12 vértices de los tres rectángulos áureos coinciden con los centros de las caras de un dodecaedro. Imagen: Wikipedia

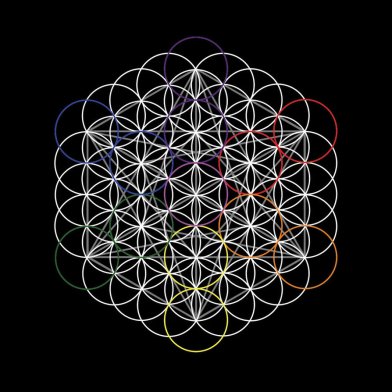
La Flor de la Vida

La Flor de la Vida es una figura conocida desde la antigüedad, y ha sido estudiada y aplicada desde entonces en diversas formas y usos. Esta figura contiene ciertas características geométricas que han llamado la atención del propio Leonardo da Vinci.

Dibujos de Leonardo Davinci — Dibujos de Leonardo da Vinci

La Flor de la Vida es una figura compuesta por 19 círculos completos del mismo diámetro y 36 arcos circulares que forman un conjunto de forma hexagonal, el cual se incluye a su vez en un círculo mayor. Los 19 círculos de la figura se solapan creando patrones radiales simétricos similares a flores de 6 pétalos.

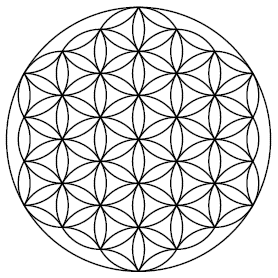
No obstante su antigüedad, su denominación «Flor de la Vida» es relativamente reciente, encontrándose muy difundida entre divulgadores de temáticas místicas y esotéricas en el contexto del movimiento Nueva Era.

Los esotéricos tienen la creencia que la Flor de la Vida es el código o matriz que el espíritu universal diseñó para poder crear y manifestar todo lo que existe en el universo.

Para ellos este código es el patrón original a través del cual la vertiente divina crea, expande y desarrolla absolutamente toda manifestación de vida. Todo lo que existe, todo lo que es, nació y nacerá a partir de esta matriz.

Diseños Derivados de la Flor de la Vida

Desagregando esta figura geométrica se pueden obtener otras figuras vinculadas:

Composición Gométrica Flor de la Vida — Figuras vinculadas a la Flor de la Vida

La «Semilla de la Vida», es el patrón base de la Flor de la Vida configurando una única "flor" con 7 círculos solapados y otro mayor que los contiene.
El «Huevo de la Vida», similar al anterior pero sin el solapamiento de los círculos.
El "Fruto de la Vida" está compuesto por 13 círculos en función a los ejes del diseño de la Flor de la Vida.

Fruto de la Vida y el cubo de Metratrón

En el marco del conocimiento esotérico se dice que el Fruto de la Vida es el plano del universo, conteniendo la estructura de cada átomo, molécula y toda forma de vida.

Asimismo, el Fruto de la Vida estaría íntimamente relacionado con los 5 Sólidos Platónicos (tetraedro, cubo, octaedro, dodecaedro e icosaedro) y se dice que contiene la base geométrica para la delineación del Cubo de Metatrón.

Si cada círculo se considera un "nodo", y se conecta con el siguiente mediante una única línea recta, se crean un total de 78 líneas, generando lo que se denomina "Cubo de Metratón", el cual contiene los modelos dimensionales de los cinco sólidos platónicos.

Metatrón

En algunas ramas del cristianismo y del judaísmo, Metatrón es el nombre de un arcángel. Sin embargo, no hay ninguna referencia a él en el Tanaj (el Antiguo Testamento de los cristianos) ni en el Nuevo Testamento cristiano.

En la versión talmúdica leída por el erudito karaíta Kirkisani, Metatrón es una figura misteriosa llamada «Yhwh menor». Curiosamente, el término hebreo metatrón es numéricamente equivalente a Shaddai, de acuerdo con la gematría hebrea.

Flor de la Vida y el cubo de Metatron — Flor de la Vida y el cubo de Metatrón

De acuerdo con una doctrina judía, Enoc fue llevado por Yahweh y transformado en Metatrón. Sin embargo, esta opinión no es compartida por muchas autoridades talmúdicas. También parece que existen dos Metatrones, uno de siete letras y otro de seis. El primero sería el Metatrón primordial y el segundo Enoc.

El Zohar llama a Metatrón «el Joven», y lo identifica como el ángel que guió al pueblo de Israel en el desierto, luego del éxodo desde Egipto, y lo describe como un sacerdote celestial. También se menciona a Metatrón en los Seudoepígrafos, principalmente en el hebreo Libro de Enoc (también llamado el Tercer Enoc), en el cual reaparece su título como «el YHWH menor».

De acuerdo con Johann Eisenmenger, Metatrón transmite las órdenes diarias de Yahwéh a los ángeles Gabriel y Rafael. A veces a Metatrón se lo identifica como hermano gemelo de Sandalfón, quien se dice que fue el profeta Elías. Según el escritor Robert Graves, el término metatron sería una corrupción hebrea del griego metradromos ('el que persigue con venganza') o de meta ton thronón ('más cercano al trono').

Conceptos vinculados con la Flor de la Vida

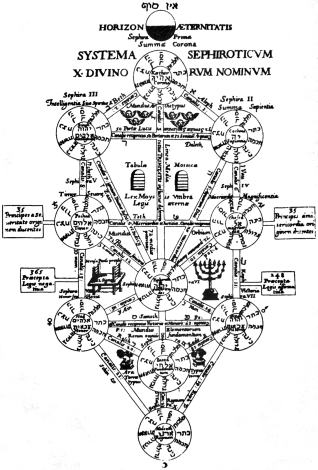
El símbolo de la Flor de la Vida puede contener en su geometría al Árbol de la Vida, por lo que se dice que esté deriva del anterior.

El Árbol de la Vida es un concepto ampliamente difundido dentro de la Kabbalah, que se utiliza para comprender la naturaleza de Dios y la manera en que creó todo lo que existe.

Arbol de la Vida de la Kabbalah — Árbol de la Vida de la Kabbalah

Los kabbalistas desarrollaron este concepto dentro de un modelo completo de la realidad, usando el árbol para representar un "mapa" de la creación, representando su "cosmovisión".

Hay quienes creen que el Árbol de la Vida de la Cábala corresponde al Árbol de la Vida mencionado en Génesis.

Arbol de la Vida - Cabala — Árbol de la Vida – Cabala

El cristianismo también tiene conexiones simbólicas con la Flor de la Vida, y en particular con la Semilla de la Vida. El símbolo del pez que se utiliza para representar a la Cristiandad encuentra sus proporciones en ésta última.

Aplicaciones ornamentales de la Flor de la Vida

El símbolo de la Flor de la Vida ha sido venerado por culturas de todo el mundo, que a falta de registros escritos, vaya uno a saber con que significado en particular. Lo que sí está claro es que ha sido empleado desde la antigüedad como motivo para ornamentar toda clase de edificios religiosos y esotéricos.

La Flor de la Vida ha sido utilizada en lugares tan distantes y disimiles como España, Escocia, Austria, Egipto, China, Turquía, Israel, India, México, entre otros.

Ephesus - Izmir, Turquía — Ephesus – Izmir, Turquía

León guardián de la Ciudad Prohibida – Beijing, China — León/perro Fu guardián de la Ciudad Prohibida – Beijing, China.

Puerta de Nínive - Louvre, Paris — Puerta de Nínive – Louvre, Paris

Templo Dorado en la India — Templo Dorado en Amistar, India

Pintura de la flor de la vida con inscripciones en hebreo.

Osirión de Abydos, Egipto

De todas las representaciones conocidas de este símbolo, la más antigua y enigmática es la del Osirión de Abydos, Egipto. El Osirión es el templo dedicado a Osiris, ya que según la mitología egipcia, fue en Abydos donde Isis encontró la cabeza de Osiris, quien había sido descuartizado por su hermano Seth. Por eso Abydos fue el centro de adoración de Osiris, señor del mundo terrenal.

El patrón de la «Flor de la Vida» está representado varias veces, con distintos niveles de intensidad, con un color rojizo sobre uno de los pilares del templo. Su diseño y trazo son absolutamente perfectos, como estampados con un molde.

Los dibujos están acompañados por una inscripción en griego que dice: "Theos Nilos", que se traduce como: "Dios del Nilo". La verdad es que por la intensidad de la tinta y el estilo (a mano alzada), el texto no parece tener el mismo origen que los símbolos, por lo que no sería acertado vincularlo para establecer la antigüedad de estos ejemplares de la Flor de la Vida.

El Osirion fue excavado por primera vez por los egiptólogos Flinders Petrie y Margaret Murray hacia 1903. En un informe publicado posteriormente, Murray dice haber encontrado graffitis de origen fenicio, griego y copto sobre las piedras del complejo egipcio.

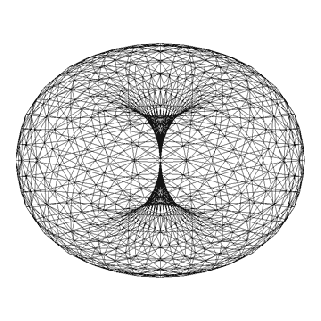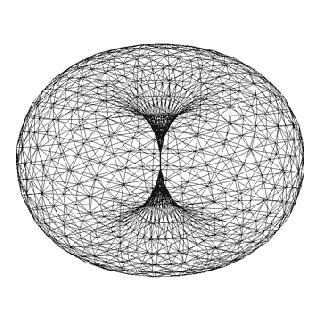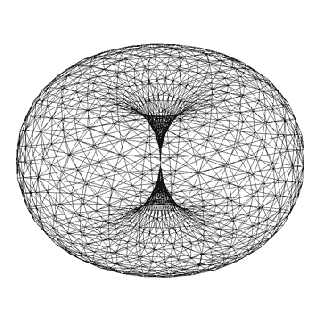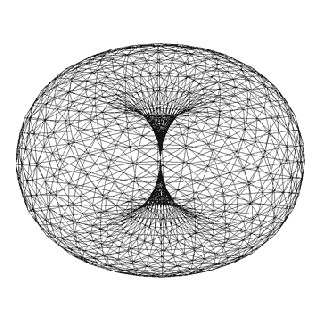
El Toroide

La Energía Toroidal esta basada en un vórtice en forma de dona en el cual la energía fluye sobre su mismo eje en una sucesión infinita.

Un toroide consta de un eje central por donde fluye la energía, desde un extremo al otro, y un campo circundante coherente. El Toroide está en perpetuo equilibrio, completitud y movimiento y sería unos de los modelos que utiliza la naturaleza para manifestarse.

El científico y filósofo Arthur Young, explica que un toroide es el único patrón de energía o dinámica que puede sostenerse a sí mismo (auto-sustentable) y está hecho de la misma sustancia que el entorno, como un tornado, del aire, y un remolino, del agua.

La Tierra con su campo magnético – Toroide

Su forma varía de tipo "rosquilla" a tipo "esfera", en función del radio de su eje, y dependiendo del medio en el que se genera. Un anillo de humo en el aire adquiere forma de rosquilla, mientras que una manzana toma una forma más esférica.

Se denomina "Punto Cero" al instante medio del eje central, en el cual las fuerzas de tracción/expulsión se neutralizan, y del cual surge todo el sistema toroidal.

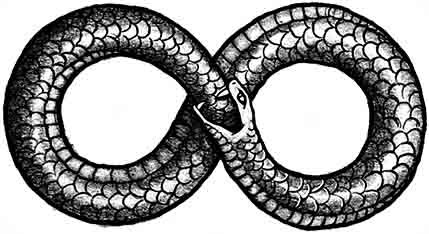
La idea de lo infinito, con un punto cero donde se neutralizan las fuerzas y donde todo comienza/termina es un concepto muy antiguo. El Uróboros es un símbolo que muestra a un animal serpentiforme, engullendo su propia cola, conformando con su cuerpo una forma circular o de "8".

El uróboros es un concepto empleado en diversas y distantes culturas ancestrales desde hace por lo menos 3000 años. En algunas de sus representaciones lleva por complemento la inscripción que dice: "el Uno es el Todo", "Todo parte del Uno y vuelve al Uno, para el Uno, por el Uno y en el Uno".

Los huracanes, los tornados, los campos magnéticos de los planetas y de las estrellas, y galaxias en sí, son todos los sistemas de energía toroidal.

El Universo es una fábrica de toroides a distintas escalas, en constante expansión y contracción produciendo la tensión necesaria para perpetuar el funcionamiento del sistema.

Un fragmento del documental "Thrive", el cual no comparto en gran medida, pero que hace foco en los conceptos de la Flor de la Vida y la energía toroidal:

Fuentes principales: