La búsqueda de la configuración óptima
Nueve triángulos en un círculo
Interconexiones
La primera clave: concurrencia
El uno y muchos
La segunda clave: concentricidad
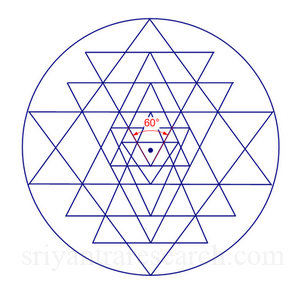
La tercera clave: triángulo interior equilátero Centro de masa El templo Sri Yantra del templo Sringeri
Los tres sabores del Sri Yantra
El óptimo Sri Yantra
La búsqueda de la configuración óptima
Si alguna vez ha intentado dibujar esta figura, ya sabe que es mucho más difícil de dibujar de lo que podría haber pensado al principio. La razón de esto es principalmente porque los triángulos están interconectados. Si mueve uno, debe mover todos los demás para que se crucen correctamente. Con suficiente tiempo o con la ayuda de computadoras y matemáticas, es posible dibujar una figura donde las intersecciones coincidan perfectamente.
Pero resulta que esto no es suficiente para definir completamente la figura. Este criterio en sí mismo no es suficiente para producir una figura única. Esta es la razón por la cual hay tantas versiones diferentes de Sri Yantra en circulación.
Sorprendentemente, los métodos que hemos encontrado en la literatura india están lejos de ser satisfactorios. A menudo conducen a cifras muy imprecisas y crudas. Solo proporcionan una idea aproximada de cómo debería ser la figura. Los métodos contemporáneos pueden conducir a cifras más precisas, pero todas son ligeramente o muy diferentes.
Esto plantea la pregunta: ¿cuál es la configuración adecuada del Sri Yantra? El objetivo de este artículo es investigar la geometría del Sri Yantra y ver si podemos encontrar más información sobre esta fascinante figura sagrada. Únase a nosotros en la búsqueda del Sri Yantra óptimo.
Preguntas que serán respondidas en este artículo:
- ¿Qué es el Sri Yantra?
- ¿Por qué es tan difícil dibujar?
- ¿Por qué hay tantas versiones diferentes?
- ¿Cuáles son las características que definen una figura óptima?
- ¿Qué es un Meru (piramidal) Sri Yantra?
- ¿Qué es un Sri Yantra Kurma (esférico)?
- ¿Cómo puedo obtener una figura óptima de Sri Yantra?
Nueve triángulos en un círculo
 |  |  |  |
| Cuatro triángulos apuntando hacia arriba. | Cinco triángulos apuntando hacia abajo | Figura central | Sri Yantra completo |
| Figura 1 | |||
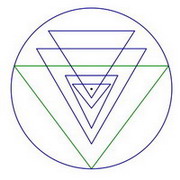
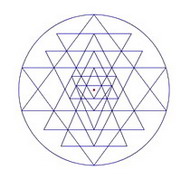
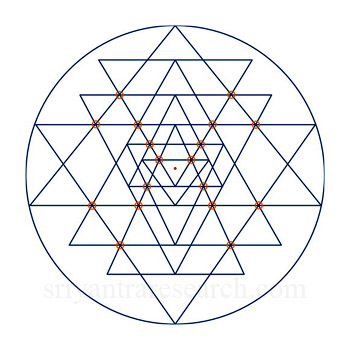
El Sri Yantra se compone de una figura central que está rodeada por dos hileras circulares de pétalos y luego por un recinto rectangular llamado bhupura. En este estudio nos centraremos principalmente en la figura central que se compone de nueve triángulos superpuestos y un punto bindu. Cuatro de los triángulos apuntan hacia arriba, los otros cinco apuntan hacia abajo. En la configuración más popular, los dos triángulos más grandes (triángulos verdes en la figura 1) tocan el círculo exterior en los tres puntos. En algunas otras versiones, hay uno o dos triángulos más que tocan el círculo exterior (ver figura 5).
 |
| Figura 2 Intersecciones triples. |
Al mirar la figura, notamos que hay un alto grado de interconexión entre los nueve triángulos. Esta es la razón principal por la que es tan difícil dibujar . Esto significa que cada triángulo está conectado a uno o más de los otros triángulos a través de puntos comunes. Cambiar la ubicación de uno de los triángulos generalmente requiere cambiar el tamaño y la posición de muchos otros triángulos.
La Figura 2 muestra dónde se encuentran los puntos de intersección triple. Estos son los puntos que unen los triángulos. No puedes mover uno sin mover también los otros.
Observe también que los dos triángulos más grandes están tocando el círculo exterior en tres puntos y que el vértice de cada triángulo está conectado a la base de otro triángulo.
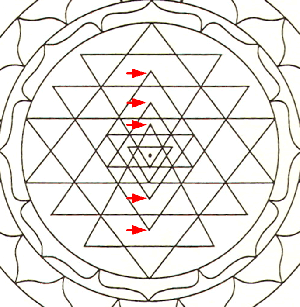 |
| Figura 3 Falso Sri Yantra |
Como con todo lo demás, existe una tendencia a simplificar y / o distorsionar las cosas , de modo que con el tiempo el conocimiento se erosiona. En el caso del Sri Yantra, esto ha llevado a lo que algunos llaman el "falso Sri Yantra". Es una versión que está tan lejos de la figura original que le falta algunas de las características más básicas de un Sri Yantra. Un ejemplo de tal Sri Yantra falso se muestra en la figura 3. Aquí vemos que el vértice de la mayoría de los triángulos no está conectado con la base de otro triángulo como lo indican las flechas rojas. Esto reduce en gran medida la dificultad de dibujar la figura y conduce a algo que se parece a un Sri Yantra pero no lo es.
La primera clave: concurrencia
 |
| Figura 4 Los errores en el dibujo conducirán a triángulos secundarios extraños. |
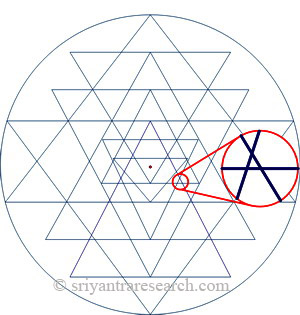
El desafío obvio al dibujar un Sri Yantra es lograr una concurrencia casi perfecta. Lo que significa que todas las intersecciones triples se encuentran en el mismo punto en lugar de entrecruzarse.
La Figura 4 muestra un detalle de un Sri Yantra con el error encerrado en rojo. Las líneas deben cruzarse en el mismo punto pero en cambio se entrecruzan y forman un triángulo extraño. El uso de la secuencia correcta para dibujar el Sri Yantra garantizará que solo haya errores en dos de las intersecciones triples.
Muy pocos Sri Yantras logran una concurrencia perfecta . Matemáticamente hablando no es posible. Pero prácticamente hablando se puede lograr un nivel satisfactorio de precisión. Es difícil lograr esto cuando se hace el dibujo a mano, pero no imposible. A menudo, las líneas se hacen más gruesas para ocultar los errores en las intersecciones. Se puede lograr un buen nivel de precisión con un lápiz y una regla y mucha paciencia. Se puede lograr una mayor precisión con un programa de dibujo como AutoCAD o Visio. La mayor precisión se logrará mediante el uso de un programa matemático como Mathematica para calcular la figura.
 |  |  |
| Figura 5 Tres configuraciones diferentes de Sri Yantra. | ||
En este punto, parece que todo lo que hay que hacer es asegurarse de que las líneas coinciden exactamente en las intersecciones triples (concurrencia) y nuestro trabajo está hecho. ¡No tan!
¿Por qué hay tantas versiones diferentes de Sri Yantra por ahí? La Figura 5 muestra algunos ejemplos de Sri Yantras. En estos ejemplos las diferencias son obvias. Las diferencias suelen ser más sutiles y requieren un examen más detallado. Al igual que los copos de nieve, parece haber un número infinito de Sri Yantras diferentes. ¿Porqué es eso? ¿Como puede ser? ¿No hay un método preciso y completo que nos diga cómo se debe dibujar esta famosa figura sagrada? Si hay uno, aún no lo hemos encontrado.
El motivo es simple. El criterio de concurrencia (intersecciones precisas) no es suficiente para definir completamente el Sri Yantra . Con el tiempo, la gente ha asumido que ser capaz de producir una figura donde las líneas se unen precisamente en las intersecciones producirá una figura única. Esto ha llevado a la multiplicidad actual de cifras disponibles.
Tomemos el ejemplo simple de dibujar un triángulo. Si el único criterio requerido es que la figura debe tener tres lados, puede dibujar un número infinito de triángulos diferentes con tres lados. Si, por otro lado, se le pide que dibuje un triángulo donde los lados tengan la misma longitud, entonces solo hay una forma de dibujar dicho triángulo (sin tener en cuenta el tamaño).
El Sri Yantra es una geometría con cinco grados de libertad , lo que significa que se pueden utilizar hasta cinco criterios diferentes para definirlo. Es por eso que tenemos que decidir la ubicación de cinco líneas al dibujar la figura. Cinco grados de libertad no es mucho considerando que hay un total de nueve triángulos. Esto se debe al alto grado de interconexión entre los triángulos. Esto efectivamente limita las posibilidades y variaciones que se pueden lograr.
La segunda clave: concentricidad
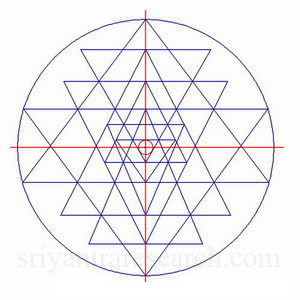 |
| Figura 6 Concentricidad: el centro del triángulo más interno coincide con el centro del círculo exterior. |
Veamos ahora el punto bindu; El pequeño punto ubicado en el triángulo central. Debe ubicarse en el centro del triángulo más interno. Esto se puede lograr precisamente colocando el bindu en el centro de un círculo que encaje dentro de este triángulo (ver figura 9). Esto se conoce en matemáticas como el incentro de un triángulo.
Sin embargo, para lograr una figura perfectamente centrada, el bindu también debe ubicarse en el centro del círculo exterior. Esto se ilustra en la figura 6. La cruz roja muestra dónde se encuentra el centro del círculo exterior. El pequeño círculo rojo muestra dónde está el centro del triángulo más interno. Como podemos ver en esta figura, coinciden. Este no es el caso para la mayoría de los Sri Yantras.
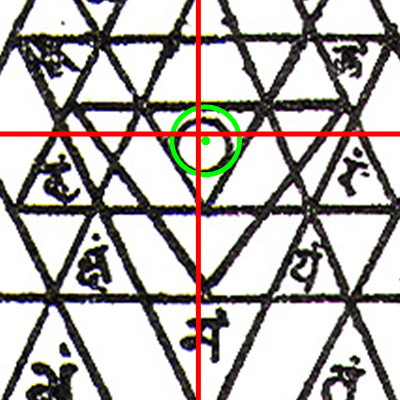 |
| Figura 7 Sri Yantra que no cumple con los criterios de concentricidad. |
La Figura 7 muestra un ejemplo de un Sri Yantra donde el centro del triángulo más interno no coincide perfectamente con el centro del círculo exterior. El punto verde (centro del triángulo más interno) no está alineado con el centro de la cruz roja (centro del círculo exterior).
La tercera clave: triángulo interno equilátero
 |
| Figura 8 R. Buckminster Fuller se para frente a su cúpula geodésica. |
El triángulo equilátero es una estructura perfecta y mínima. Es la estructura más simple, fuerte y fundamental en geometría y gráficos por computadora. Tiene el mayor grado de tensegridad para una cantidad mínima de elementos estructurales. Por eso es tan frecuente en los diseños estructurales creados por Buckminster Fuller. Esta es también la razón por la cual la cúpula geodésica , una estructura esférica compuesta de pequeños triángulos, es la única estructura hecha por el hombre que se vuelve proporcionalmente más fuerte a medida que aumenta de tamaño.
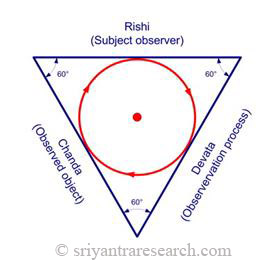 |
| Figura 9 Triángulo equilátero como la expresión de Rishi, Devata, Chanda. |
El Sri Yantra simboliza, entre otras cosas, el desarrollo de la creación. El bindu representa lo no manifestado, el estado silencioso. El siguiente nivel en la expresión del Universo está representado por el triángulo más interno. Este nivel representa la trinidad de rishi, devata, chanda o el observador, el proceso de observación y el objeto que se observa. En este punto, la simetría de la creación aún está intacta y se romperá cuando alcance el siguiente nivel que representa los aspectos más groseros del pariente.
Esto refleja el desarrollo de la unidad a la trinidad como se expone en la literatura védica. Según el Veda, el Universo se manifiesta cuando la conciencia ilimitada se da cuenta de sí misma. La chispa de la autoconciencia enciende la creación. En este punto, la Unidad se divide en la trinidad de rishi (el observador), devata (proceso de conocimiento) y chanda (el objeto de percepción). La misma idea también se encuentra en la Biblia como el principio de la santa trinidad.
El triángulo central es la lente central del Sri Yantra. Si, como sugieren algunos, este patrón es capaz de emitir una cantidad significativa de energía sutil, la importancia de tener una figura bien equilibrada y centrada se hace evidente.
Por estas razones, creemos que el triángulo central debe ser equilátero en una configuración óptima de Sri Yantra. Para que esto suceda, el triángulo primario que apunta hacia abajo más alto debe tener un ángulo de 60 grados (consulte las figuras 9 y 11).
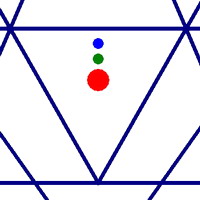 |  |  |
| Figura 10 | ||
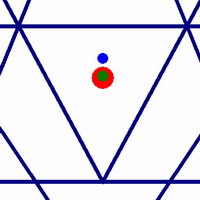
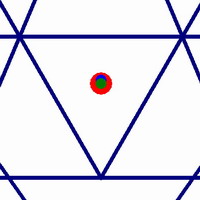
Ahora veamos si podemos encontrar formas de confirmar la idea de que nos estamos acercando a una configuración perfectamente equilibrada. Otra medida del equilibrio general de una estructura es el centro de masa. Este es el punto en la geometría donde se equilibraría si fuera un objeto sólido.
La Figura 10 muestra una vista detallada del triángulo central de tres Sri Yantras diferentes. La figura de la izquierda muestra una configuración donde solo se logra la concurrencia . En este caso, el bindu (punto rojo), el centro del círculo exterior (punto verde) y el centro de masa (punto azul) no están alineados.
La figura central muestra un Sri Yantra que logra concurrencia y concentricidad . Como resultado, el bindu (rojo) y el centro del círculo exterior (verde) se superponen muy bien. Sin embargo, el centro de masa todavía no se superpone.
A la derecha vemos que para una figura dibujada con los tres criterios que hemos sugerido ( concurrencia, concentricidad y triángulo central equilátero ), los tres centros se superponen y tenemos una figura perfectamente centrada y equilibrada.
El Sri Yantra del Templo Sringeri
 |  |
| Figura 11 Sri Yantra del templo Sringeri . | |
El templo Sringeri en India afirma tener el Sri Yantra más antiguo. Este templo es uno de los cuatro pilares fundados por nada menos que Shankara durante el primer milenio. Asumiendo que los Sri Yantras más antiguos están más cerca de la configuración original, veamos cómo este Sri Yantra se compara con nuestra versión óptima. Obviamente no es posible estar seguro de que es el Sri Yantra más antiguo de la Tierra, pero ciertamente es más antiguo que la mayoría de las versiones disponibles. La forma de los pétalos y el bhupura son buenos indicadores de que es una configuración antigua de Sri Yantra.
La Figura 11 muestra una supuesta imagen de este Sri Yantra y un diagrama que se extrajo de la imagen. Teniendo en cuenta las distorsiones causadas por la cámara y la impresión, podemos ver que la figura tiene muchas de las mismas características que nuestra figura óptima. El bindu está bien centrado y, lo que es más importante, el triángulo más central tiene un ángulo muy cercano a 60 grados.
Los tres sabores del Sri Yantra
 |  |  |
| Forma plana | Forma piramidal (Meru) | Forma esférica (Kurma) |
Dado que Sri Yantra se basa en triángulos, es muy apropiado que actualmente haya tres formas principales de representar esta figura. La primera y probablemente la más común es la forma plana , que es lo que hemos estado viendo hasta ahora. Más fotos de la forma del avión se pueden ver aquí .
La segunda es la forma piramidal llamada Meru en India. El monte Meru es una montaña mítica. Llamado así por la forma de la montaña de la figura. Más fotos de Sri Yantras piramidales se pueden ver aquí .
La tercera y más rara forma es la forma esférica o Kurma . Kurma fue la segunda encarnación de Vishnu, la encarnación de la tortuga. Esto se refiere a la similitud entre esta forma y el caparazón de una tortuga. Es interesante notar que parece haber cierta confusión con el uso de estos dos términos. La forma piramidal a menudo se denomina erróneamente Kurma. Esta forma es la más rara debido al extremadamente alto nivel de dificultad que implica generarlo. Todavía no hemos encontrado una representación física correcta de un Sri Yantra esférico. Hay muchos intentos, pero muy pocos han tenido éxito. Aquí se pueden ver imágenes de Sri Yantras esféricas .
Como hemos mencionado anteriormente, dibujar un Sri Yantra con errores mínimos en las intersecciones es en sí mismo un buen desafío. Si además de eso agregamos los dos criterios adicionales que hemos propuesto (concentricidad, y triángulo interno equilátero), entonces probablemente tomaría toda una vida de pruebas y errores para lograr tal cifra. Pero gracias a las computadoras y las matemáticas esto se puede lograr en un abrir y cerrar de ojos. Sin embargo, para lograr este resultado, la figura debe convertirse en una ecuación simultánea y luego resolverse para las restricciones requeridas. Para más información sobre este tema, eche un vistazo al excelente artículode CS Rao. Una vez hecho esto, podemos dar forma a la figura de acuerdo con los diferentes criterios descritos anteriormente para obtener una figura óptima donde los errores en las intersecciones son mínimos, la figura está perfectamente centrada y el triángulo más interno es equilátero.
| if you like slowest version - https://www.youtube.com/watch?v=0eTVHoxqZYM www.youtube.com |
| SRI YANTRA MEDITATION 528 HZ & 432 HZ | Sri Yantra Power For Meditation | Powerful Yantra For Money - Duration: 1:11:11. SONIC ELEVATOR - POWERFUL BRAINWAVE MEDITATIONS 22,699 views www.youtube.com |